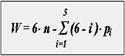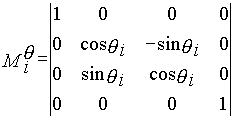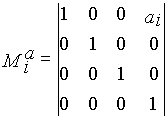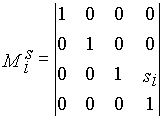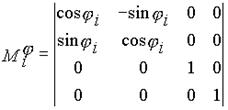Промышленные роботы и манипуляторы.
Оглавление
1. Промышленные работы и манипуляторы.
2. Назначение и области применения.
3. Классификация промышленных роботов.
4. Принципиальное устройство промышленного робота.
5. Основные понятия и определения.
Промышленный робот
– автоматическая машина, состоящая из манипулятора и устройства программного
управления его движением, предназначенная для замены человека при выполнении
основных и вспомогательных операций в производственных процессах.
Манипулятор – совокупность пространственного рычажного
механизма и системы приводов, осуществляющая под управлением
программируемого автоматического устройства или человека-оператора действия
(манипуляции), аналогичные действиям руки человека.
Назначение и область применения.
Промышленные роботы предназначены для замены человека при выполнении основных и вспомогательных технологических операций в процессе промышленного производства. При этом решается важная социальная задача - освобождения человека от работ, связанных с опасностями для здоровья или с тяжелым физическим трудом, а также от простых монотонных операций, не требующих высокой квалификации. Гибкие автоматизированные производства, создаваемые на базе промышленных роботов, позволяют решать задачи автоматизации на предприятиях с широкой номенклатурой продукции при мелкосерийном и штучном производстве. Копирующие манипуляторы, управляемые человеком-оператором, необходимы при выполнении различных работ с радиоактивными материалами. Кроме того, эти устройства незаменимы при выполнении работ в космосе, под водой, в химически активных средах. Таким образом, промышленные роботы и копирующие манипуляторы являются важными составными частями современного промышленного производства.
Классификация промышленных роботов.
Промышленные роботы классифицируются по следующим признакам:
|
· по характеру выполняемых технологических операций · основные; · вспомогательные; · универсальные; · по виду производства · литейные; · сварочные; · кузнечно-прессовые; · для механической обработки; · сборочные; · окрасочные; · транспортно-складские; · по системе координат руки манипулятора · прямоугольная; · цилиндрическая; · сферическая; · сферическая угловая (ангулярная); · другие; · по числу подвижностей манипулятора; · по грузоподъемности · сверхлегкие (до 10 Н); · легкие (до 100 Н); · средние (до 2000 Н); · тяжелые (до 10000 Н); · сверхтяжелые (свыше 10000 Н); · по типу силового привода · электромеханический; · пневматический; · гидравлический; · комбинированный; · по подвижности основания · мобильные; · стационарные; · по виду программы · с жесткой программой; · перепрограммируемые; · адаптивные; · с элементами искусственного интеллекта; · по характеру программирования · позиционное; · контурное; · комбинированное. |
Принципиальное устройство промышленного робота.
Манипулятор промышленного робота по своему функциональному
назначению должен обеспечивать движение выходного звена и, закрепленного в
нем, объекта манипулирования в пространстве по заданной траектории и с
заданной ориентацией. Для полного выполнения этого требования основной
рычажный механизм манипулятора должен иметь не менее шести подвижностей,
причем движение по каждой из них должно быть управляемым. Промышленный робот
с шестью подвижностями является сложной автоматической системой. Эта система
сложна как в изготовлении, так и в эксплуатации. Поэтому в реальных
конструкциях промышленных роботов часто используются механизмы с числом
подвижностей менее шести. Наиболее простые манипуляторы имеют три, реже две,
подвижности. Такие манипуляторы значительно дешевле в изготовлении и
эксплуатации, но предъявляют специфические требования к организации рабочей
среды. Эти требования связаны с заданной ориентацией объектов
манипулирования относительно механизма робота. Поэтому оборудование должно
располагаться относительно такого робота с требуемой ориентацией.
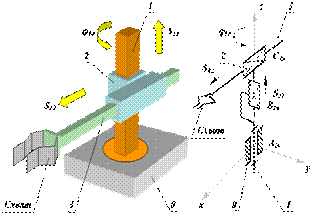
Рассмотрим для примера структурную и функциональную схемы
промышленного робота с трехподвижным манипулятором. Основной механизм руки
манипулятора состоит из неподвижного звена 0 и трех подвижных звеньев 1, 2 и
3 (рис.19.1).
Рис. 19.1
|
|
|
|
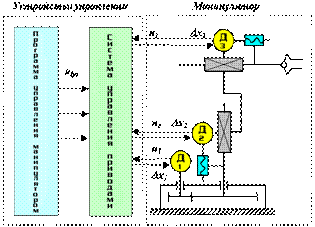
Механизм этого манипулятора соответствует цилиндрической системе координат. В этой системе звено 1 может вращаться относительно звена 0 (относительное угловое перемещение j10), звено 2 перемещается по вертикали относительно звена 1 (относительное линейное перемещение S21) и звено 3 перемещается в горизонтальной плоскости относительно звена 2 (относительное линейное перемещение S32). На конце звена 3 укреплено захватное устройство или схват, предназначенный для захвата и удержания объекта манипулирования при работе манипулятора. Звенья основного рычажного механизма манипулятора образуют между собой три одноподвижные кинематические пары (одну вращательную А и две поступательные В и С) и могут обеспечить перемещение объекта в пространстве без управления его ориентацией. Для выполнения каждого из трех относительных движений манипулятор должен быть оснащен приводами, которые состоят двигателей с редуктором и системы датчиков обратной связи. Так как движение объекта осуществляется по заданному закону движения, то в системе должны быть устройства сохраняющие и задающие программу движения, которые назовем программоносителями. При управлении от ЭВМ такими устройствами могут быть дискеты, диски CD, магнитные ленты и др. Преобразование заданной программы движения в сигналы управления двигателями осуществляется системой управления. Эта система включает ЭВМ, с соответствующим программным обеспечением, цифроаналоговые преобразователи и усилители. Система управления, в соответствии с заданной программой, формирует и выдает на исполнительные устройства приводов (двигатели) управляющие воздействия ui. При необходимости она корректирует эти воздействия по сигналам Dxi, которые поступают в нее с датчиков обратной связи. Функциональная схема промышленного робота приведена на рис. 19.2.
|
|
|
|
Основные
понятия и определения. Структура манипуляторов.
Геометро-кинематические характеристики.
Формула строения - математическая запись структурной схемы манипулятора, содержащая информацию о числе его подвижностей, виде кинематических пар и их ориентации относительно осей базовой системы координат (системы, связанной с неподвижным звеном).
Движения, которые обеспечиваются манипулятором делятся на:
· глобальные (для роботов с подвижным основанием) - движения стойки манипулятора, которые существенно превышают размеры механизма;
· региональные (транспортные) - движения, обеспечиваемые первыми тремя звеньями манипулятора или его "рукой", величина которых сопоставима с размерами механизма;
· локальные (ориентирующие) - движения, обеспечиваемые звеньями манипулятора, которые образуют его "кисть", величина которых значительно меньше размеров механизма.
В соответствии с этой классификацией движений, в манипуляторе
можно выделить два участка кинематической цепи с различными функциями:
механизм руки и механизм кисти. Под "рукой" понимают ту часть манипулятора,
которая обеспечивает перемещение центра схвата – точки М (региональные
движения схвата); под "кистью" – те звенья и пары, которые обеспечивают
ориентацию схвата (локальные движения схвата).
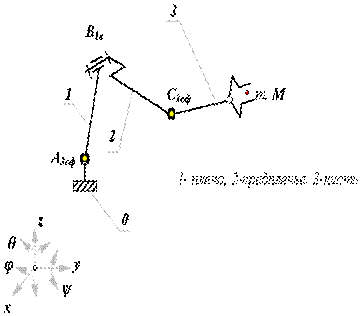
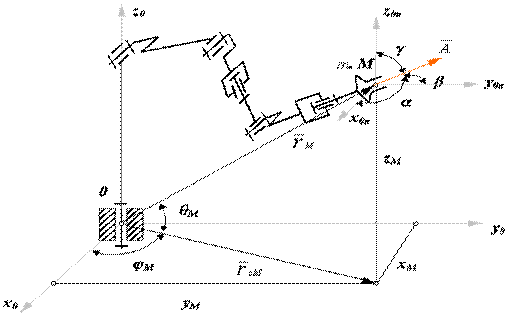
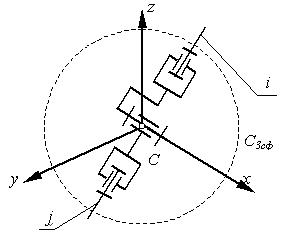
Рассмотрим структурную схему антропоморфного манипулятора, то есть схему
которая в первом приближении соответствует механизму руки человека
(рис.19.3).
|
|
|
|
Этот механизм состоит из трех подвижных звеньев и трех кинематических пар: двух трех подвижных сферических А3сф и С3сф и одной одноподвижной вращательной В1в.
Кинематические пары манипулятора характеризуются: именем или
обозначением КП - заглавная буква латинского алфавита (A,B,C и т.д.);
звеньями, которые образуют пару (0/1,1/2 и т.п.); относительным движением
звеньев в паре ( для одноподвижных пар - вращательное, поступательное и
винтовое); подвижностью КП (для низших пар от 1 до 3, для высших пар от 4 до
5); осью ориентации оси КП относительно осей базовой или локальной системы
координат.
Рабочее пространство манипулятора - часть пространства,
ограниченная поверхностями огибающими к множеству возможных положений его
звеньев.
Зона обслуживания манипулятора - часть пространства
соответствующая множеству возможных положений центра схвата манипулятора.
Зона обслуживания является важной характеристикой манипулятора. Она
определяется структурой и системой координат руки манипулятора, а также
конструктивными ограничениями наложенными относительные перемещения звеньев
в КП.
Подвижность манипулятора W - число независимых обобщенных
координат однозначно определяющее положение схвата в пространстве.
|
|
или для незамкнутых кинематических цепей:
|
|
Маневренность манипулятора М - подвижность манипулятора при зафиксированном (неподвижном) схвате.
|
|
Возможность изменения ориентации схвата при размещении его центра в заданной точке зоны обслуживания характеризуется углом сервиса - телесным углом y, который может описать последнее звено манипулятора (звено на котором закреплен схват) при фиксации центра схвата в заданной точке зоны обслуживания.
|
|
где: fC - площадь сферической поверхности, описываемая точкой С звена 3, lCM- длина звена 3.
Относительная величина ky = y / (4p), называется коэффициентом сервиса.. Для манипулятора, изображенного на рис.19.4,
|
подвижность манипулятора: W = 6 * 3 - (3 * 2 - 5 * 1) = 18 - 11 = 7; маневренность: M = 7 - 6 = 1; формула строения: W = [q10 + j10 + y10 ] + j21 + [q32 + j32 + y32 ]. |
|
|
|
|
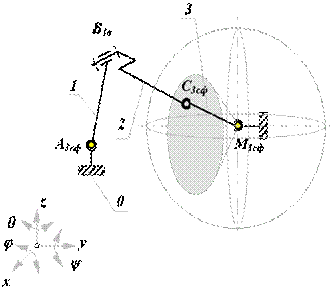
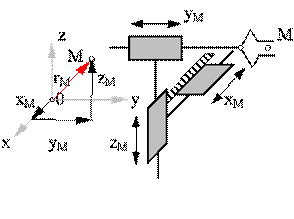
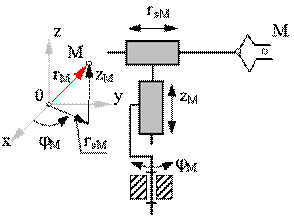
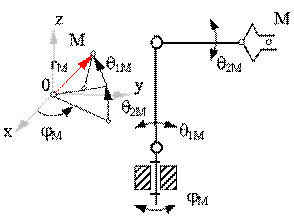
Структура кинематической цепи манипулятора должна обеспечивать требуемое перемещение объекта в пространстве с заданной ориентацией. Для этого необходимо, чтобы схват манипулятора имел возможность выполнять движения минимум по шести координатам: трем линейным и трем угловым. Рассмотрим на объекте манипулирования точку М, которая совпадает с центром схвата. Положение объекта в неподвижной (базовой) системе координат 0x0y0z0 определяется радиусом-вектором точки М и ориентацией единичного вектора с началом в этой точке. В математике положение точки в пространстве задается в одной из трех систем координат:
· прямоугольной декартовой с координатами xM, yM, zM;
· цилиндрической с координатами rsM, j M, zM;
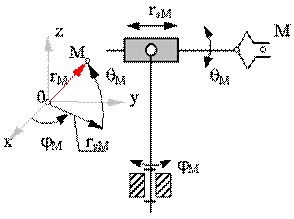
· сферической с координатами rM, j M, q M.
Ориентация объекта в пространстве задается углами a, b и g, которые вектор ориентации образует с осями базовой системы координат. На рис. 19.5 дана схема шести подвижного манипулятора с вращательными кинематическими парами с координатами объекта манипулирования.
|
|
|
|
При структурном синтезе механизма манипулятора необходимо учитывать следующее:
· кинематические пары манипуляторов снабжаются приводами, включающими двигатели и тормозные устройства, поэтому в схемах манипуляторов обычно используются одноподвижные кинематические пары: вращательные или поступательные;
· необходимо обеспечить не только заданную подвижность свата манипулятора, но и такую ориентацию осей кинематических пар, которая обеспечивала необходимую форму зоны обслуживания, а также простоту и удобство программирования его движений;
· при выборе ориентации кинематических пар необходимо учитывать расположение приводов (на основании или на подвижных звеньях), а также способ уравновешивания сил веса звеньев.
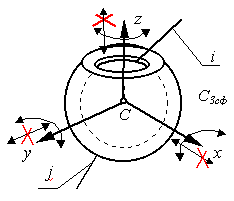
При выполнении первого условия кинематические пары с
несколькими подвижностями заменяют эквивалентными кинематическими
соединениями. Пример такого соединения для сферической пары дан на рис.
19.6.
Перемещение схвата в пространстве можно обеспечить, если ориентировать оси
первых трех кинематических пар по осям одной из осей координат. При этом
выбор системы координат определяет тип руки манипулятора и вид его зоны
обслуживания. По ГОСТ 25685-83 определены виды систем координат для руки
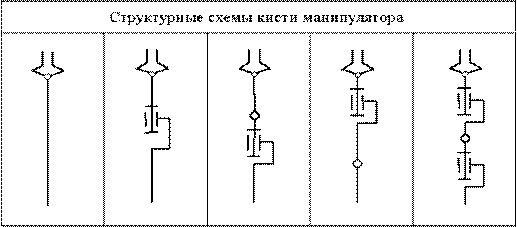
манипулятора, которые приведены в таблице 19.1. Здесь даны примеры
структурных схем механизмов соответствующие системам координат. Структурные
схемы механизмов кисти, применяемые в манипуляторах, даны в таблице 19.2.
Присоединяя к выходному звену руки тот или иной механизм кисти, можно
получить большинство известных структурных схем манипуляторов, которые
применяются в реальных промышленных роботах.
|
|
|
|
Сферическая кинематическая |
Эквивалентное кинематическое |
Рис. 19.6
|
Системы координат "руки" манипулятора. |
|
Прямоугольная (декартова) |
Цилиндрическая |
|
|
|
|
Сферическая |
Угловая (ангулярная) |
|
|
|
|
Другие |
|
|
|
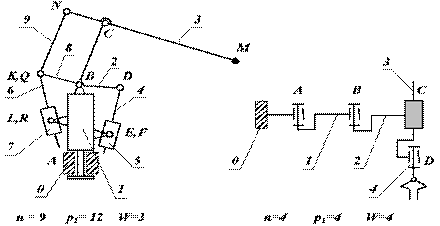
Структура манипулятора определяется и местом размещения приводов. Если приводы размещаются непосредственно в кинематических парах, то к массам подвижных звеньев манипулятора добавляются массы приводов. Суммарная нагрузка на приводы и их мощность увеличиваются, а отношение массы манипулятора к полезной нагрузке (максимальной массе объекта манипулирования) уменьшается. Поэтому при проектировании роботов приводы звеньев руки, как наиболее мощные и обладающие большей массой, стремятся разместить ближе к основанию робота. Для передачи движения от привода к звену используются дополнительные кинематические цепи. Рассмотрим схему руки манипулятора ПР фирмы ASEA (рис.19.7). К трехзвенному механизму с ангулярной системой координат добавлены:
· для привода звена 2 - простейший кулисный механизм, образованный звеньями 4,5 и 2;
· для привода звена 3 - цепь, состоящая из кулисного механизма (звенья 6,7 и 8) и шарнирного четырехзвенника (звенья 8,9,2 и 3).
Таким образом, в рычажном механизме можно выделить
кинематическую цепь руки (звенья 1,2 и 3) и кинематические цепи приводов.
Манипуляторы использующие принцип размещения приводов на основании имеют
более сложные механизмы. Однако увеличение числа звеньев и кинематических
пар компенсируется уменьшением масс и моментов инерции, подвижных звеньев
манипулятора. Кроме того, замкнутые кинематические цепи повышают точность и
жесткость механизма. В целом манипуляторы, использующие принципы
комбинированного размещения приводов (часть приводов на основании, часть на
подвижных звеньях), обладают лучшими энергетическими и динамическими
характеристиками, а также более высокой точностью.
В кинематических схемах рассмотренных манипуляторов веса звеньев вызывают
дополнительную нагрузку на приводы. Фирма SKILAM разработала робот
SANCIO (рис. 19.8) в котором веса приводов и звеньев воспринимаются
кинематическими парами, а на момент двигателей влияют только через силы
трения. Такая структурная схема механизма потребовала увеличения размеров
кинематических пар, однако в целом был получен существенный выигрыш по
энергетическим и динамическим показателям.
Данные примеры не охватывают всех возможных ситуаций рационального выбора
структуры манипуляторов. Они только демонстрируют наиболее известные из
удачных структурных схем.
|
|
|
|
|
|
Рис. 19.8 |
|
Важная особенность манипуляторов – изменение структуры
механизма в процессе работы, о чем говорилось на лекции по структуре
механизмов. В соответствии с циклограммой или программой работы робота, в
некоторых кинематических парах включаются тормозные устройства. При этом два
звена механизма жестко соединяются с друг другом, образуя одно звено. Из
структурной схемы механизма исключается одна кинематическая пара и одно
звено, число подвижностей схвата механизма уменьшается (обычно на единицу).
Изменяется структура механизма и в тех случаях, когда в процессе выполнения
рабочих операций (на пример, при сборке или сварке) схват с объектом
манипулирования соприкасается с окружающими предметами, образуя с ними
кинематические пары. Кинематическая цепь механизма замыкается, а число
подвижностей уменьшается. В этом случае в цепи могут возникать избыточные
связи. Эти структурные особенности манипуляторов необходимо учитывать при
программировании работы промышленного робота.
Быстродействие ПР определяют максимальной скоростью линейных перемещений
центра схвата манипулятора. Различают ПР с малым (VM<0.5 м/с),
средним (0.5 < VM < 1.0 м/с) и высоким (VM>1.0м/с)
быстродействием. Современные ПР имеют в основном среднее быстродействие и
только около 20% - высокое.
Точность манипулятора ПР характеризуется абсолютной линейной погрешностью
позиционирования центра схвата. Промышленные роботы делятся на группы с
малой (D
rM< 1 мм), средней (0.1 мм <
D
rM < 1 мм) и высокой (D
rM< 0.1 мм) точностью позиционирования.
Задачи механики манипуляторов.
К основным задачам механики манипуляторов можно отнести:
|
· манипразработку методов синтеза и анализа исполнительных механизмов (включая механизмы приводов); · программирование движения манипулятора; · расчет управляющих усилий и реакций в КП; · уравновешивание механизмов манипуляторов; · другие задачи. |
Эти задачи решаются на базе общих методов исследования структуры, геометрии, кинематики и динамики систем с пространственными много подвижными механизмами. Каждая из рассматриваемых задач может быть сформулирована как прямая (задача анализа) или как обратная (задача синтеза). При определении функций положения механизма, в прямой задаче находят закон изменения абсолютных координат выходного звена по заданным законам изменения относительных или абсолютных координат звеньев. В обратной – по заданному закону движения схвата находят законы изменения координат звеньев, обычно, линейных или угловых перемещений в приводах. Решение обратной задачи или задачи синтеза более сложно, так как часто она имеет множество допустимых решений, из которых необходимо выбрать оптимальное. В обратной задаче кинематики по требуемому закону изменения скоростей и ускорений выходного звена определяются соответствующие законы изменения скоростей и ускорений в приводах манипулятора. Обратная задача динамики заключается в определении закона изменения управляющих сил и моментов в приводах, обеспечивающих заданный закон движения выходного звена.
Кинематический анализ механизма манипулятора.
Первая и основная задача кинематики – определение функции
положения. Для пространственных механизмов наиболее эффективными методами
решения этой задачи являются векторный метод и метод преобразования
координат. При решении прямой задачи о положении схвата манипулятора обычно
используют метод преобразования координат. Из множества методов
преобразования координат [ 1, 2 ] , которые отличаются друг от друга
правилами выбора осей локальных систем координат, для манипуляторов обычно
используется метод Денавита и Хартенберга.
Опишем два вида матриц:
матрицы М, определяющие отношение между системами координат
соседних звеньев;
матрицы Т, определяющие положение и ориентацию каждого звена
механизма в неподвижной или базовой системе координат.
Воспользуемся однородными координатами трехмерного проективного пространства
РR3, в которых движение евклидова пространства
R3 можно, представить линейным преобразованием
![]() где
Мij – матрица 4x4 вида .
где
Мij – матрица 4x4 вида .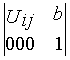
Это преобразование эквивалентно преобразованию в евклидовом
пространстве
![]() где
где ![]() .
То есть преобразованию, которое включает поворот, определяемый матрицей
Uij размерностью 3х3, и параллельный
перенос, задаваемый вектором
.
То есть преобразованию, которое включает поворот, определяемый матрицей
Uij размерностью 3х3, и параллельный
перенос, задаваемый вектором ![]() размерностью
3. В однородном пространстве положение точки будут определять
не три x, y и z, а четыре величины x', y',
z' и t', которые удовлетворяют следующим соотношениям:
размерностью
3. В однородном пространстве положение точки будут определять
не три x, y и z, а четыре величины x', y',
z' и t', которые удовлетворяют следующим соотношениям:
x = x'/t', y = y'/t', z = z'/t'.
Обычно принимают t'=1. У матрицы поворота
Uij элементами uij являются
направляющие косинусы углов между новой осью i и старой осью
j. Вектор ![]() -
трехмерный вектор, определяющий положение начала новой системы координат
i в старой системе j. Выбор расположения осей
должен соответствовать решаемой задаче. При решении задачи о положениях
необходимо: в прямой задаче определить положение выходного звена как функцию
перемещений в приводах, в обратной – заданное положение выходного звена
представить как функцию перемещений в приводах. Выбор расположения и
ориентации локальных систем координат должен обеспечивать выполнение этих
задач. При использовании метода Денавита и Хартенберга оси координат
располагаются по следующим правилам:
-
трехмерный вектор, определяющий положение начала новой системы координат
i в старой системе j. Выбор расположения осей
должен соответствовать решаемой задаче. При решении задачи о положениях
необходимо: в прямой задаче определить положение выходного звена как функцию
перемещений в приводах, в обратной – заданное положение выходного звена
представить как функцию перемещений в приводах. Выбор расположения и
ориентации локальных систем координат должен обеспечивать выполнение этих
задач. При использовании метода Денавита и Хартенберга оси координат
располагаются по следующим правилам:
1. Для звена i ось
zi направляется по оси кинематической пары,
образуемой им со звеном (i+1). Начало координат размещают в
геометрическом центре этой пары.
2. Ось xi направляется по общему
перпендикуляру к осям zi-1 и zi
с направлением от zi-1 к zi.
Если оси zi-1 и zi
совпадают, то xi перпендикулярна к ним и направлена
произвольно. Если они пересекаются в центре кинематической пары, то начало
координат располагается в точке пересечения, а ось xi
направляется по правилу векторного произведения (кратчайший
поворот оси zi до совмещения с zi-1
при наблюдении с конца xi должен происходить против
часовой стрелки).
3. Ось yi направляется так, чтобы система
координат была правой.
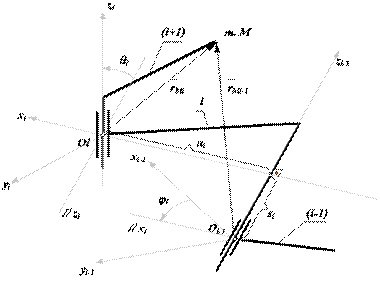
В прямой задаче необходимо определить положение схвата манипулятора и связанной с ним системы координат Mxnynzn по отношению к неподвижной или базовой системе координат Kx0y0z0. Это осуществляется последовательными переходами из системы координат звена i в систему координат звена i-1. Согласно принятому методу, каждый переход включает в себя последовательность четырех движений: двух поворотов и двух параллельных переносов, осуществляемых в указанной последовательности (см. рис. 20.1):
· поворот i-ой системы вокруг оси xi на угол -qi до параллельности осей zi и zi-1 (положительное направление поворота при наблюдении с конца вектора xi против часовой стрелки);
· перенос вдоль оси xi на величину -ai до совмещения начала системы координат Oi с точкой пересечения осей xi и zi-1 (отсчет по оси xi от точки пересечения оси xi и оси zi-1);
|
|
|
|
· перенос вдоль оси zi-1 на величину -si, после которого начало системы координат Oi оказывается в начале координат Oi-1 системы (i-1) (отсчитывается по оси zi-1 от ее начала координат Oi-1 до точки ее пересечения с осью xi);
· поворот вокруг оси zi-1 на угол -ji, до тех пор пока ось xi не станет параллельной оси xi-1 (положительное направление поворота при наблюдении с конца вектора zi-1 против часовой стрелки).
Необходимо отметить, что знак угла поворота не имеет
значения, так как в матрицах перехода используются направляющие косинусы
(четные функции). Целесообразно рассматривать угол, обеспечивающий
кратчайший поворот оси старой системы i до совмещения
(параллельности) с соответствующей осью новой (i-1).
Перемещения начала координат определяются как координаты начала старой
системы Oi в новой Oi-1.
В манипуляторах обычно используются одноподвижные кинематические пары или
вращательные, или поступательные. Оба относительных движения как
вращательное , так и поступательное, реализуются в цилиндрических парах.
Поэтому при общем представлении механизма используются (рис.20.1)
цилиндрические пары.
Матрицы перехода их системы Oi в систему Oi-1
можно записать так:
![]() ,
,
|
где: |
|
- матрица поворота вокруг оси xiна угол -qi, |
|
|
|
- матрица переноса вдоль оси xi на -ai, |
|
|
|
- матрица переноса вдоль оси zi-1 на -si, |
|
|
|
- матрица поворота вокруг оси zi-1 на угол -ji. |
В этих матрицах переменные si и
ji
соответствуют относительным перемещениям звеньев в кинематических парах и
являются обобщенными координатами манипулятора, определяющими конфигурацию
механизма в рассматриваемом положении. Переменные ai
и qi
определяются конструктивным исполнением звеньев манипулятора, в процессе
движения они остаются неизменными.
Положение некоторой произвольной точки М в системе координат
звена i определяется вектором rMi, а
в системе координат звена (i-1) – вектором rMi-1.
Эти радиусы связаны между собой через матрицу преобразования координат
Мi следующим уравнением:
![]() ,
,
|
где: |
|
- матрица перехода из i-ой системы координат в (i - 1)-ю. |
Рассмотрим шести подвижный манипулятор в исходном или начальном положении (рис.20.2). За начальное положение принимается такое, в котором все относительные обобщенные координаты равны нулю. Переход из системы координат любого i–го звена к неподвижной или базовой системе записывается в виде
![]() или
,
или
,![]()
где![]() -
матрица преобразования координат i–ой системы в координаты
базовой системы координат.
-
матрица преобразования координат i–ой системы в координаты
базовой системы координат.
|
|
|
|
Для схемы, изображенной на рис.20.2, радиус rM6 = 0, а радиус rM0 определится по формуле, то есть положение выходного звена манипулятора определяется матрицей Тn. Элементы этой матрицы определяют положение центра схвата точки М и ориентацию его в пространстве. Четвертый столбец определяет, декартовы координаты точки М (проекции вектора rM0на оси координат). Третий столбец содержит направляющие косинусы оси zn системы координат, связанной со схватом, или вектора подхода , который характеризует направление губок схвата (рис.20.3). Второй столбец определяет направление оси yn или вектора ориентации , который проходит через центр схвата по оси перпендикулярной рабочим поверхностям его губок. В первом столбце содержатся направляющие косинусы оси xn или вектора . Углом подхода схвата называется угол между вектором подхода и базовым вектором, где - орт вектора неподвижной или базовой системы координат. С учетом сказанного, матрица Tn может быть представлена в следующем виде
|
|
|
|
В результате матричных преобразований получаем радиус-вектор точки М схвата в функции обобщенных координат. Обычно, за обобщенные координаты принимают линейные и угловые перемещения в кинематических парах или на выходных валах приводов манипулятора. В механизме с n подвижностями в общем виде функцию положения схвата можно записать так
где q1, q2, … qn – обобщенные координаты манипулятора.
При кинематическом анализе манипулятора в прямой задаче необходимо определить линейные и угловые скорости и ускорения схвата при заданных угловых и линейных обобщенных скоростях и ускорениях (обычно относительных скоростях и ускорениях в кинематических парах механизма). В обратной задаче по заданному закону изменения скоростей и ускорений схвата определяются законы изменения скоростей и ускорений в КП или на выходных звеньях приводов. Решение прямой задачи кинематики для точки М схвата можно получить продифференцировав четвертый столбец матрицы Тn по времени
|
|
Угловую скорость и угловое ускорение схвата можно определить векторным суммированием относительных угловых скоростей во вращательных КП механизма. Так как вектора угловых скоростей, при данном выборе ориентации осей координат, совпадают с осью z, то угловая скорость схвата, где орт оси z системы координат, расположенной в центре КП, соединяющей звено i и звено i-1, m – число вращательных КП в механизме. Дифференцируя это выражение по времени, получим формулу для определения углового ускорения схвата: где орт оси z системы координат, расположенной в центре КП, соединяющей звено i и звено i-1, m – число вращательных КП в механизме. Дифференцируя это выражение по времени, получим формулу для определения углового ускорения схвата:
Динамика манипуляторов
промышленных роботов.
Силовой расчет манипулятора.
Из большого разнообразия задач динамики манипуляторов рассмотрим две: силовой расчет и расчет быстродействия ПР. При силовом расчете манипуляторов решается задачи по определению внешних силовых управляющих воздействий, обеспечивающих требуемый закон движения механизма, и по расчету реакций в кинематических парах. Первую часть часто называют задачей синтеза управления . При силовом расчете обычно применяется метод кинетостатики, основанный на принципе Д’Аламбера. По этому методу к внешним силам и моментам, приложенным к звеньям механизма, добавляются расчетные силы инерции, которые обеспечивают силовую уравновешенность системы и позволяют рассматривать подвижную систему в квазистатическом равновесии, то есть, как условно неподвижную. Силовой расчет выполняется при заданной полезной нагрузке , известных законах движения звеньев и (из предварительного кинематического расчета), известных инерционных характеристиках звеньев: массах звеньев mi и их моментах инерции Isi. По этим данным определяются главные вектора и главные моменты сил инерции для каждого из звеньев механизма. Для открытой кинематической цепи решение начинаем с выходного звена – схвата. Отброшенные связи звена n со звеном n-1 и выходным валом привода звена n заменяем реакциями и и составляем кинетостатические векторные уравнения равновесия сил и моментов для звена n
где -
вектор момента в кинематической паре (проекция этого вектора на ось z
является движущим моментом привода в КП, то есть ).
|
|
Далее рассматривается равновесие звена n-1. При этом в месте его присоединения к звену n прикладываются реакции со стороны звена равные по величине и противоположные по направлению реакциям, определенным на предыдущем этапе расчета. Так последовательно составляются уравнения силового равновесия для всех n звеньев механизма. Из решения полученной системы 6n уравнений определяются реакции в кинематических парах, движущие силы и моменты.
Расчет быстродействия промышленного робота.
Время выполнения роботом цикла перемещений детали во многом
определяет производительность всего роботизированного комплекса. Поэтому
требования к быстродействию робота обычно достаточно высокие. Время
выполнения роботом технологической операции обусловлено законами изменения
внешних сил (движущих и сопротивления) и инертностью звеньев механизма.
Закон изменения управляющих сил зависит от типа используемого привода и от
вида системы управления. Существуют роботы с гидравлическими,
пневматическими, электрическими и комбинированными приводами. В них
применяются цикловые, позиционные или контурные системы управления.
Рассмотрим расчет быстродействия одного из приводов промышленного робота с
цикловой системой управления. При цикловой системе управления относительные
перемещения звеньев ограничиваются передвижными упорами и концевыми
выключателями.
На рис. 20.5 изображена кинематическая схема трех подвижного манипулятора ПР
(1,2,3 – подвижные звенья, 0 – неподвижное звено). Здесь же приведена
циклограмма настройки командоаппарата (сплошные линии) и циклограмма работы
ПР (пунктирные линии). Общее время рабочего цикла Тц состоит из
времени выстоя в заданных положениях (на циклограмме выстой показан прямыми
параллельными горизонтальной оси t) и времени относительных перемещений
звеньев из одного заданного положения в другое tпх и обратно tох
(наклонные прямые на диаграммах ). Время выстоя обычно задано условиями
технологического процесса. Время выполнения роботом движений определяется
динамическими характеристиками приводов и манипулятора – движущими силами и
силами сопротивления, массами и моментами инерции звеньев.
|
|
Рассмотрим работу пневмопривода перемещения руки манипулятора По сигналу от командоаппарата в правую полость цилиндра подается сжатый воздух, который действует на поршень с силой Fд3 = p * Sп, где р - давление воздуха, Sп - активная площадь поршня. Под действием этой силы поршень и рука 3 перемещаются влево с постоянным ускорением и с возрастающей скоростью V32 (рис.20.6а). Ограничение хода поршня может осуществляться либо жестким упором без демпфера, либо упором с демпфером.
|
|
|
|
При остановке на упоре без демпфера , скорость звена 3 должна мгновенно уменьшится с некоторого конечного значения до нуля. При таком изменении скорости ускорение a32 стремится к бесконечности. Такая остановка звена называется жестким ударом. Она сопровождается большими динамическими нагрузками на звенья механизма. Так как реальный манипулятор представляет собой упруго-инерционную систему, то эти нагрузки вызовут отскок звена 3 от упора, а также колебания всего механизма. Схват будет совершать колебания относительно заданного конечного положения. Время затухания этого процесса Dt значительно снижает быстродействие ПР. Уменьшить эти колебания или вообще исключить их можно, обеспечив безударный останов
V32n = 0, a32n = 0;
где V32n, a32n - относительная скорость и относительное ускорение звеньев в момент останова. Однако это осуществимо только в регулируемом приводе при контурном управлении. Кроме того при безударном останове в конце хода относительная скорость близка к нулю, поэтому время перемещения схвата в требуемое положение значительно возрастает. Компромиссным решением является останов с мягким ударом, при котором относительная скорость в конце хода V32n= 0, а ускорение ограничено некоторым допустимым значением a32n <= [a] . В механизмах с цикловым управлением режим движения с мягким ударом обеспечивается установкой
|
|
|
|
Рассмотрим работу пневмопривода перемещения руки манипулятора (рис.20.5). По сигналу от командоаппарата в правую полость цилиндра подается сжатый воздух, который действует на поршень с силой Fд3 = p * Sп, где р - давление воздуха, Sп - активная площадь поршня. Под действием этой силы поршень и рука 3 перемещаются влево с постоянным ускорением и с возрастающей скоростью V32 (рис.20.6а). Ограничение хода поршня может осуществляться либо жестким упором без демпфера, либо упором с демпфером.
|
|
|
|
При остановке на упоре без демпфера , скорость звена 3 должна мгновенно уменьшится с некоторого конечного значения до нуля. При таком изменении скорости ускорение a32 стремится к бесконечности. Такая остановка звена называется жестким ударом. Она сопровождается большими динамическими нагрузками на звенья механизма. Так как реальный манипулятор представляет собой упруго-инерционную систему, то эти нагрузки вызовут отскок звена 3 от упора, а также колебания всего механизма. Схват будет совершать колебания относительно заданного конечного положения. Время затухания этого процесса Dt значительно снижает быстродействие ПР. Уменьшить эти колебания или вообще исключить их можно, обеспечив безударный останов
V32n = 0, a32n = 0;
где V32n, a32n - относительная скорость и относительное ускорение звеньев в момент останова. Однако это осуществимо только в регулируемом приводе при контурном управлении. Кроме того при безударном останове в конце хода относительная скорость близка к нулю, поэтому время перемещения схвата в требуемое положение значительно возрастает. Компромиссным решением является останов с мягким ударом, при котором относительная скорость в конце хода V32n= 0, а ускорение ограничено некоторым допустимым значением a32n <= [a] . В механизмах с цикловым управлением режим движения с мягким ударом обеспечивается установкой упоров с демпферами, гасящими кинетическую энергию руки. Расчет демпфера ведется из условия ASn =0 , которое обеспечивается равенством за цикл движения работы движущей силы AFд3 и работы силы сопротивления демпфера АFc (рис. 20.6б):
AFд3 = -АFc или Fд3 * (H32 – hд) = - Fc * hд.
В этом выражении неизвестны две величины Fc и hд, одной из них задаются, вторую – рассчитывают.
Уравновешивание манипуляторов.
В большинстве кинематических схем манипуляторов приводы воспринимают статические нагрузки от сил веса звеньев. Это требует значительного увеличения мощностей двигателей приводов и моментов тормозных устройств. Для борьбы с этим используют три метода:
Используют кинематические схемы манипуляторов, в которых силы веса звеньев воспринимаются подшипниками кинематических пар. На мощность приводов и тормозных устройств при таком решении силы веса оказывают влияние только через силы трения в парах. В качестве примера можно привести кинематическую схема робота SCARA. Недостатком этого метода являются большие осевые нагрузки в подшипниках. Уравновешивание звеньев манипулятора с помощью корректировки их массы. При этом центр масс звена с помощью корректирующих масс смещается в центр кинематической пары Недостатком этого метода является значительное увеличение массы манипулятора и моментов инерции его звеньев.
Уравновешивание сил веса звеньев манипулятора с помощью упругих разгружающих устройств – пружинных разгружателей или уравновешивателей. Эти устройства не позволяют обеспечить полную разгрузку приводов от действия сил веса на всем относительном перемещении звеньев. Поэтому конструкция этих устройств включает кулачковые или рычажные механизмы, которые согласуют упругую характеристику пружины с характеристикой уравновешиваемых сил веса звеньев. На рис. 20.9 показана схема примышленного робота в котором привод вертикального перемещения руки снабжен механизмом для силовой разгрузки, состоящим из пружины и кулачкового механизма с профилем выполненным по спирали Архимеда
Точность манипуляторов ПР.
Точность манипуляторов определяется погрешностями позиционирования характеристической точки схвата (точка М) и погрешностями угловой ориентации схвата. Погрешности позиционирования определяются технологическими отклонениями размеров звеньев манипулятора, зазорами в кинематических парах манипулятора и механизмов приводов, деформациями (упругими и температурными) звеньев, а также погрешностями системы управления и датчиков обратной связи. В паспортных данных манипуляторов указывается максимально допустимое отклонение центра схвата манипулятора точки М от ее номинального расположения на множестве возможных конфигураций механизма. В результате погрешностей точка М описывает в пространстве некоторый эллипсоид, который называется эллипсоидом отклонений.
Литература
1. Силовой расчет, уравновешивание, проектирование механизмов и механика манипуляторов: Учебное пособие для студентов смешанной формы обучения / И.Н.Чернышева, А.К.Мусатов, Н.А.Глухов и др.; Под ред. А.К.Мусатова. – М.: Изд-во МГТУ, 1990. – 80с., ил.
2. Механика промышленных роботов: Учеб. пособие для втузов: В 3-х кн. / под ред. К.В.Фролова, Е.И.Воробьева. – М.: Высш.шк., 1988.
3. Р.Пол “Моделирование, планирование траекторий и управление движением робота – манипулятора” - М.: Наука, 1976.
|